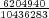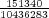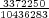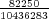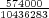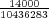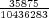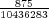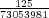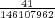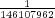Kelly Plays Powerball
by Stefan Hollos and Richard Hollos
This is part of the book, Bet Smart: The Kelly System for Gambling and Investing.
Powerball is a lottery run by the Multi-State Lottery Association (MUSL) which is made up of 31 states and the District of Columbia. MUSL is a non-profit organization which means that excess proceeds from the lottery are distributed to the association members. It is unclear what percentage of the proceeds is used for prize money but it is almost certainly less than 50 percent.
Lotteries are almost never a good bet. The odds of winning are usually very low but people are attracted to them because of the large prizes that can be won. In the case of Powerball, the grandprize can reach into the hundreds of millions of dollars. There is no rational way to justify playing a game with such bad odds but then few people view gambling as a rational pursuit. In a perfectly rational world there would be no casinos and less fun and excitement.
The one dollar that it costs to buy a single Powerball ticket has less utility to most people than the chance it brings, however small, of winning a prize in the millions of dollars. There is nothing irrational about this, up to a point. There is no shortage of stories (true or not) about people spending their last dollar on a Powerball ticket and becoming millionaires.
How much net worth should one have in order to justify the purchase of a $1 Powerball ticket? There is really no objective way to answer this question, since people have different utility functions for their money. The Kelly criterion does offer one way to calculate the required net worth for playing Powerball. The calculation is performed below, but you can see that it really makes no sense in this case. If people played Powerball using the Kelly criterion, then very few tickets would be sold, and the lottery would soon go out of business.
Is it possible to turn Powerball from a gamble into an investment? At first this sounds like an absurd question. We will show below, however, that when the grand prize becomes large enough, the expected return from playing Powerball becomes positive. At first glance therefore, it meets one of the conditions for being an investment, i.e. a positive expected return. For something to be considered an investment, however, the positive returns must be realized in a reasonable amount of time. Playing Powerball does not come anywhere close to meeting this condition. On average, the game would have to be played at very high grand prize levels for thousands of years before the positive expected returns could be realized. Powerball is a perfect illustration of the fact that a positive expected return is not enough. You also need to be able to realize the return in a reasonable amount of time.
We will start our Powerball analysis by describing the mechanics of how the game is played. In a Powerball drawing, 5 numbers are chosen from the numbers 1 through 55, and then there is a separate drawing of one number from the numbers 1 through 42. This last single number is called the Powerball number. The actual process of drawing the numbers involves randomly choosing 5 white balls from a drum of 55 white balls marked with the numbers 1 through 55. The Powerball number is gotten by randomly choosing 1 red ball from a separate drum of 42 red balls marked with the numbers 1 through 42.
You play the game by purchasing a ticket with 5 numbers chosen from 1 through 55, and a Powerball number chosen from 1 through 42. There can be no duplicates in the 5 numbers that you choose. You can either choose the numbers yourself, or you can have a computer randomly choose the numbers for you when you purchase the ticket. The cost of a single ticket is $1. The prizes are awarded based upon how many of the 5 numbers you match with the drawing, and whether or not you match the Powerball number. The value of the grand prize is determined by how many tickets are sold, while the values of the lesser prizes are fixed. For an extra $1 you have the option of multiplying the lesser prizes by a randomly chosen factor of 2 through 5. This is called the powerplay option.
The table below shows the prizes associated with the different ways of matching the numbers in the drawing. The wb column refers to how many of the 5 white ball numbers are matched, and the pb column refers to whether or not the Powerball is matched, with 1 meaning a match, and 0 no match. Note that not all possible ways of matching are awarded a prize.
|
To calculate the probabilities of winning each of the prizes, you have to determine how many ways the matches can be made, and also how many unique possible tickets there are. You also have to keep in mind that the order of the numbers in the drawing and on the tickets is irrelevant. In other words, a permutation of the 5 numbers in the drawing or on the ticket does not count as a different set of numbers. The total number of ways of choosing 5 numbers from the set of numbers 1 through 55 is equal to
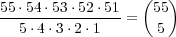 | (1) |
where we have used the binomial coefficient notation defined as
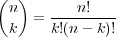 | (2) |
The number of ways of choosing the Powerball from the numbers 1 through 42 is just 42. The total number of possible unique tickets is then
 | (3) |
Now the number of ways of matching exactly n of the 5 white balls in a drawing is given by
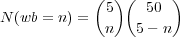 | (4) |
so that the probability of matching exactly n white balls
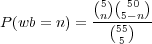 | (5) |
where n = 0,1,…,5. The probability of matching the Powerball is
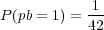 | (6) |
and the probability of not matching the Powerball is
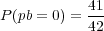 | (7) |
The following table lists all the possible outcomes of a drawing along with their probabilities, and odds.
|
The overall chance of winning 1 of the 9 prizes is equal to
 | (8) |
and the overall chance of not winning anything is
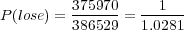 | (9) |
Let us imagine now that exactly 1 of every possible Powerball ticket was sold. The total proceeds from the ticket sales would be $146,107,962. How large can the grand prize be for the lottery just to break even? The total amount of money the lottery would have to pay out in this case is $28,800,030 + GP. Setting this equal to the total ticket sales, and solving for GP gives a maximum grand prize of GP = $117,307,932. It turns out that this is also the value of the grand prize, above which, the expected return becomes positive. Of course since probably no more than 50% of ticket sales revenue goes towards prizes, the grand prize in this case would be much less.
Calculating the expected return, using the probabilities and prize values, gives us the following function
 | (10) |
The expectation is zero when the grand prize is equal to $117,307,932. When the grand prize is below this value, you will lose money in the long run. When it is above this value, you will make money in the long run. You have to be careful about the term ’long run’ here. What it means is that you would have to play the game for thousands of years with the jackpot being greater than 117 million each time in order to realize a positive expected return.
Now let’s look at what the Kelly criterion has to say about playing Powerball and one’s net worth. The Kelly fraction for any gamble or investment is the largest fraction of one’s assets that can be put into play without risking ruin. If you calculate the Kelly fraction for Powerball, then assuming only one ticket is purchased for $1, the required net worth to play the game according to the Kelly criterion would be one over the fraction. Figure 1 shows the required net worth as a function of the grand prize. Note that at a grandprize value of $117,307,932 the minimum worth is ∞ because the expectation is zero. The Kelly criterion is very misleading in this case however. Since the time scale for realizing expectations is so long, and net worth tends to grow with time from other sources, there is no chance of ruin from playing $1 Powerball games unless one’s net worth is extremely small.